Encuestas Sociales
Juan Carlos Castillo
Sociología FACSO - UChile
2do Sem 2022
encuestas-sociales.netlify.com
Sesión 11: Análisis factorial

De la clase anterior ...

Preguntas y error de medición
Para medir hechos observables simples usualmente se utiliza una pregunta (ej: edad)
Fenómenos complejos se miden en general con más de una pregunta, con el objetivo de dar mejor cuenta del atributo (i.e. minimizar error de medición)
Preguntas y error de medición
En este marco se asume que el indicador es distinto del atributo, y que la medición del atributo o variable latente conlleva error
Cuando la el atributo se mide con más de una pregunta, se puede intentar estimar la variable latente mediante índices o técnicas de análisis factorial
Construcción de índices
análisis descriptivo de items (ej: plot_stackfrq de sjPlot)
matriz de correlaciones (ej: con
corrplot)cálculo de consistencia interna (Alpha de Cronbach)
cálculo de índice promedio (atendiendo casos perdidos)
Esta clase: Análisis factorial
Variables latentes (1)
La mayor parte de las variables en el mundo social no son directamente observables. Esto las hace constructos hipotéticos latentes
La medición de variables latentes se realiza a partir de indicadores observables, tales como los ítems de una batería/ cuestionario
Variables latentes (2)
Lo latente puede ser entendido como la varianza compartida por diferentes indicadores observados
La medición de variables latentes se encuentra asociada al modelo de factor común (Thurstone) y al análisis factorial
Factor común
Cada indicador en un set de medidas observadas es una función linealde uno o más factores comunes y un factor único
Como referencia podemos usar la teoría clásica de test (CTT), que divide el puntaje de los indicadores entre puntaje verdadero y error
Factor común
Cada indicador en un set de medidas observadas es una función linealde uno o más factores comunes y un factor único
Como referencia podemos usar la teoría clásica de test (CTT), que divide el puntaje de los indicadores entre puntaje verdadero y error
X=T+E
σ2x=σ2t+σ2e
Donde
- X= puntaje observado,
- T= puntaje verdadero, y
- E= error
Modelo de factor común
La existencia de un solo ítem por constructo no permite aislar puntaje verdadero del error
Si existen más ítems, el análisis factorial y distinguir entre varianza común (compartida con otros indicadores) y varianza única (o error)
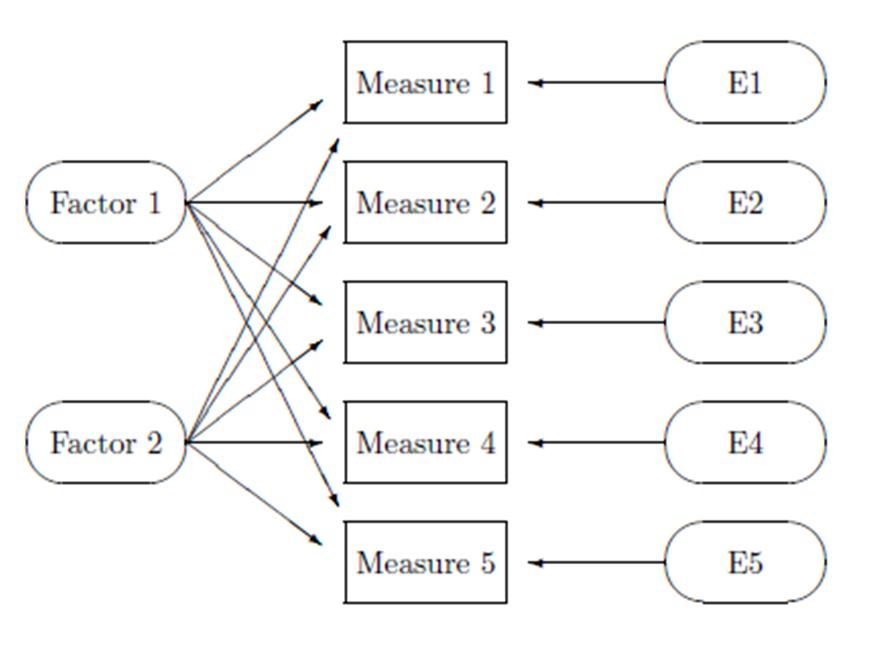
Análisis factorial
Es un método que permite:
identificar la varianza común a una serie de indicadores
establecer la contribución de cada indicador a la varianza común
estimar posteriormente un índice (puntaje factorial) para cada factor, con mayor precisión que un promedio bruto
Análisis factorial
Un factor es una variable no observada o latente que da cuenta de las correlaciones entre indicadores
los indicadores están correlacionados porque comparten una causa común - concepto de independencia condicional
El o los factores darían cuenta (i.e. causarían) de la covariación entre una serie de medidas observadas (indicadores)
Objetivos del análisis factorial
Teórico: relacionar datos con dimensiones latentes basadas en conceptos (validez de constructo)
Pragmático: hacer sentido de un conjunto de datos, reducción de dimensiones y obtención de puntajes
Metodológico: aislar el error (varianza única) de la varianza común
Alternativas en análisis factorial
exploratorio (EFA): Permite explorar las dimensiones que subyacen a una escala
confirmatorio (CFA): Permite confirmar las dimensiones que subyacen a una escala, aislando el error de medición en la estimación
Análisis factorial exploratorio (EFA)
Forma de análisis factorial donde se estiman la o las variables latentes a un conjunto de indicadores, sin una especificación previa de la estructura factorial.
Preguntas a responder:
¿Cuántos factores subyacen a un conjunto de indicadores?
¿Cómo se relacionan los indicadores con los factores?
¿Cómo es la calidad del modelo estimado?
Características EFA

Basado en la matriz de correlaciones
Modelo estandarizado (varianza factores=1)
Diferentes métodos de extracción de factores
Determinación del número y "calidad" de las dimensiones (continuas) subyacentes a una escala
Ejemplo Brown 2006 (Chap.2)
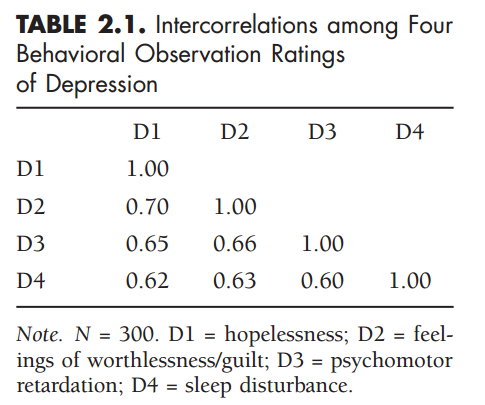
Ejemplo Brown 2006 (Chap.2)
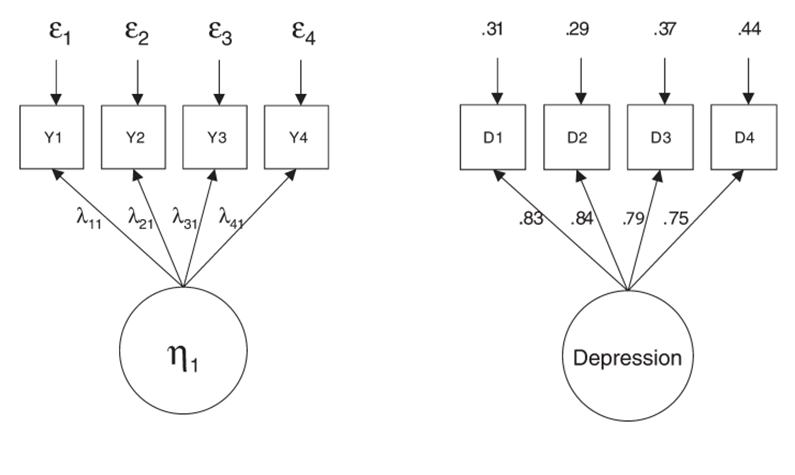
Modelo estadístico
yj=λj1η1+λj2η2+...+λjmηm+εj
Donde
η : factor
λjm : carga factorial que relaciona al indicador j con el factor η
εj : varianza que es única al indicador yj
... aplicado al ejemplo de Brown 2006:
- D1=λ11η1+ε1
- D2=λ21η1+ε2
- D3=λ31η1+ε3
- D4=λ41η1+ε4
Aplicado al ejemplo de Brown 2006:
Reproduccion de matriz de correlaciones a patir de los parámetros del modelo. Ejemplo Brown 2006 cap. 2:
VAR(D1)= σ11=λ11ψ11+ε1=.832(1)+.31=1.00
COV(D1,D2)= σ21=λ11ψ11λ21=(.83)(1)(.84)=.70
Conceptos y parámetros
Factores: variables latentes que están a la base de las correlaciones entre los indicadores
Cargas factoriales: medida estandarizada de asociación (correlación) entre el indicador y la variable latente
Comunalidad: proporción del indicador que se asocia a factor(es) comun(es)
Conceptos y parámetros (2)
Varianza única (uniqueness): 1-comunalidad
Eigenvalues: medida de proporción de la varianza total correspondiente a cada uno de los factor (SS loadings)
Proporción de varianza explicada por el factor = eigenvalue / número de indicadores
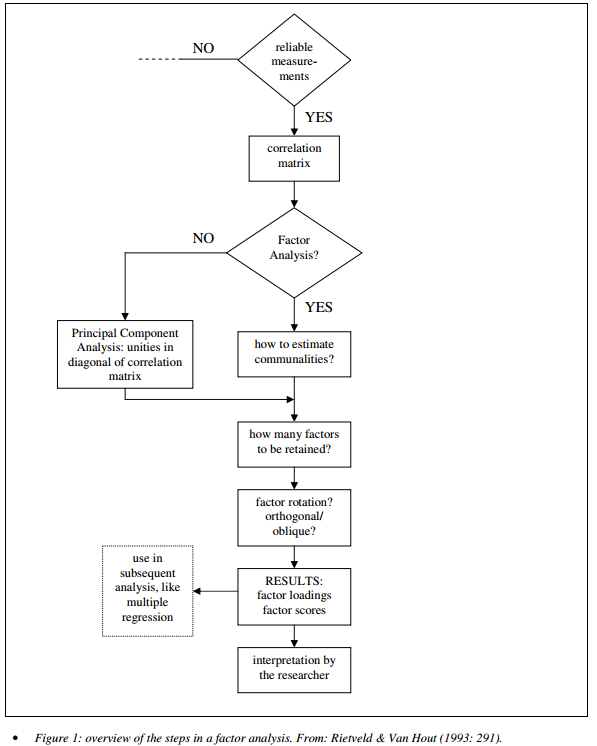
Pasos en el análisis
Estimación de matriz de correlaciones
Extraccion de factores
Decisión sobre número de factores
Rotación
Interpretación y reporte
Obtención de puntajes factoriales
Supuestos a evaluar
Nivel de medición de variables, normalidad (eventualmente test de normalidad multivariado, ej: Shapiro Wilk multivariado)
Test de adecuación muestal (KMO)
varía entre 0 y 1, contrasta si las correlaciones parciales entre las variables son pequeñas.
valores pequeños (menores a 0.5) indican que los datos no serían adecuados para EFA, ya que las correlaciones entre pares de variables no pueden ser explicadas por otras variables
Supuestos a evaluar (2)
Nivel de correlaciones de la matriz: test de esfericidad de Bartlett
se utiliza para evaluar la hipótesis que la matriz de correlaciones es una matriz identidad (diagonal 1 y bajo la diagonal 0)
se busca significación (p < 0.05)ya que se espera que las variables estén correlacionadas
Metodos de extracción
Factores principales
Factores principales iterados: estima comunalidades iterativamente, reemplazandolas en la matriz de correlaciones a partir de las comunalidades estimadas desde los factor loadings
Maximum likelihood: maximiza la posibilidad de que los parametros reproduzcan los datos observados
Instrumentos y criterios de selección del número de factores
Criterio de Kaiser: eigenvalues mayores a 1
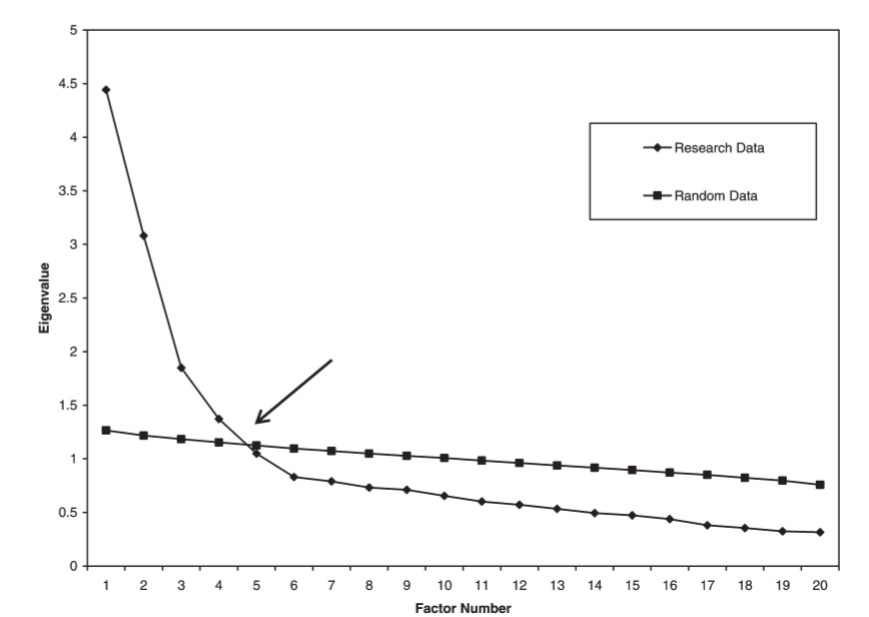
Scree plot (gráfico de sedimentación)
Análisis paralelo: comparación de eigenvalues de la muestra con eigenvalues de datos aleatorios. Nº apropiado de factores: numero de eigenvalues de los datos reales que son mayores que sus correspondientes eigenvalues de datos aleatorios
Screeplot y análisis paralelo
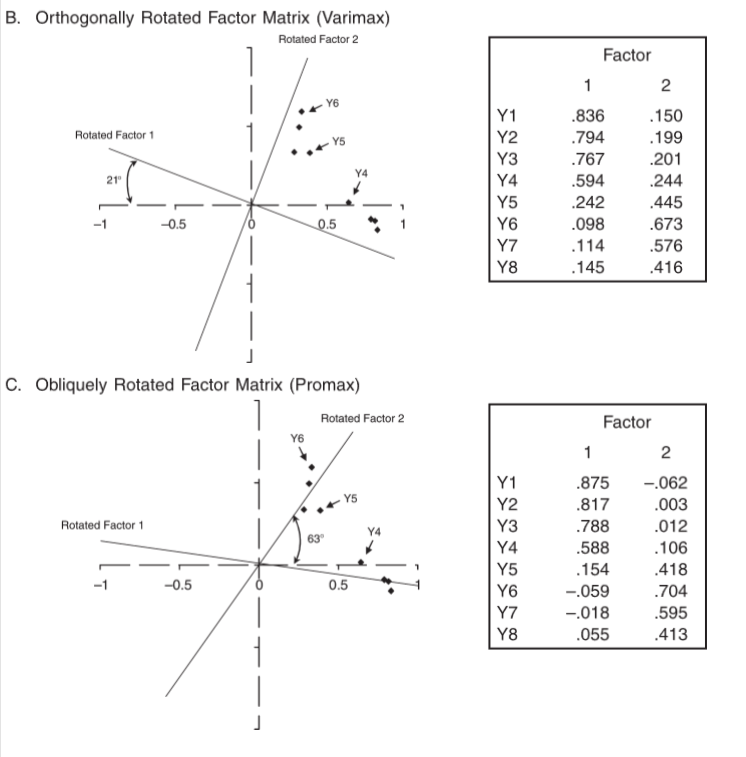
Tipos de rotación
Ortogonal: asume que los factores no se encuentran correlacionados
Oblicua: permite correlación entre factores
Resumen
dimensiones subyacentes = factores
análisis factorial
- relación entre indicadores y dimensiones
- estimación de número de dimensiones probables subyacentes a batería
- rotación
- obtención de puntajes factoriales (índices ponderados)
Encuestas Sociales
Juan Carlos Castillo
Sociología FACSO - UChile
2do Sem 2022
encuestas-sociales.netlify.com
Sesión 11: Análisis factorial